Skip to contents

Reproducing Kernel Hilbert Space (RKHS) Filters

Source: R/RKHS.R
rkhs_filter.Rd

Estimation of a filter using Reproducing Kernel Hilbert Space (RKHS)

Usage

rkhs_filter(
  horizon = 6,
  degree = 2,
  kernel = c("BiWeight", "Henderson", "Epanechnikov", "Triangular", "Uniform",
    "TriWeight"),
  asymmetricCriterion = c("Timeliness", "FrequencyResponse", "Accuracy", "Smoothness",
    "Undefined"),
  density = c("uniform", "rw"),
  passband = 2 * pi/12,
  optimalbw = TRUE,
  optimal.minBandwidth = horizon,
  optimal.maxBandwidth = 3 * horizon,
  bandwidth = horizon + 1
)

Arguments

horizon

horizon (bandwidth) of the symmetric filter.

degree

degree of polynomial.

kernel

kernel uses.

asymmetricCriterion

the criteria used to compute the optimal bandwidth. If "Undefined", \(m+1\) is used.

density

hypothesis on the spectral density: "uniform" (= white woise, the default) or "rw" (= random walk).

passband

passband threshold.

optimalbw

boolean indicating if the bandwith should be choosen by optimisation (between optimal.minBandwidth and optimal.minBandwidth using the criteria asymmetricCriterion). If optimalbw = FALSE then the bandwith specified in bandwidth will be used.

optimal.minBandwidth, optimal.maxBandwidth

the range used for the optimal bandwith selection.

bandwidth

the bandwidth to use if optimalbw = FALSE.

Value

a finite_filters() object.

References

Dagum, Estela Bee and Silvia Bianconcini (2008). “The Henderson Smoother in Reproducing Kernel Hilbert Space”. In: Journal of Business & Economic Statistics 26, pp. 536–545. URL: https://ideas.repec.org/a/bes/jnlbes/v26y2008p536-545.html.

Examples

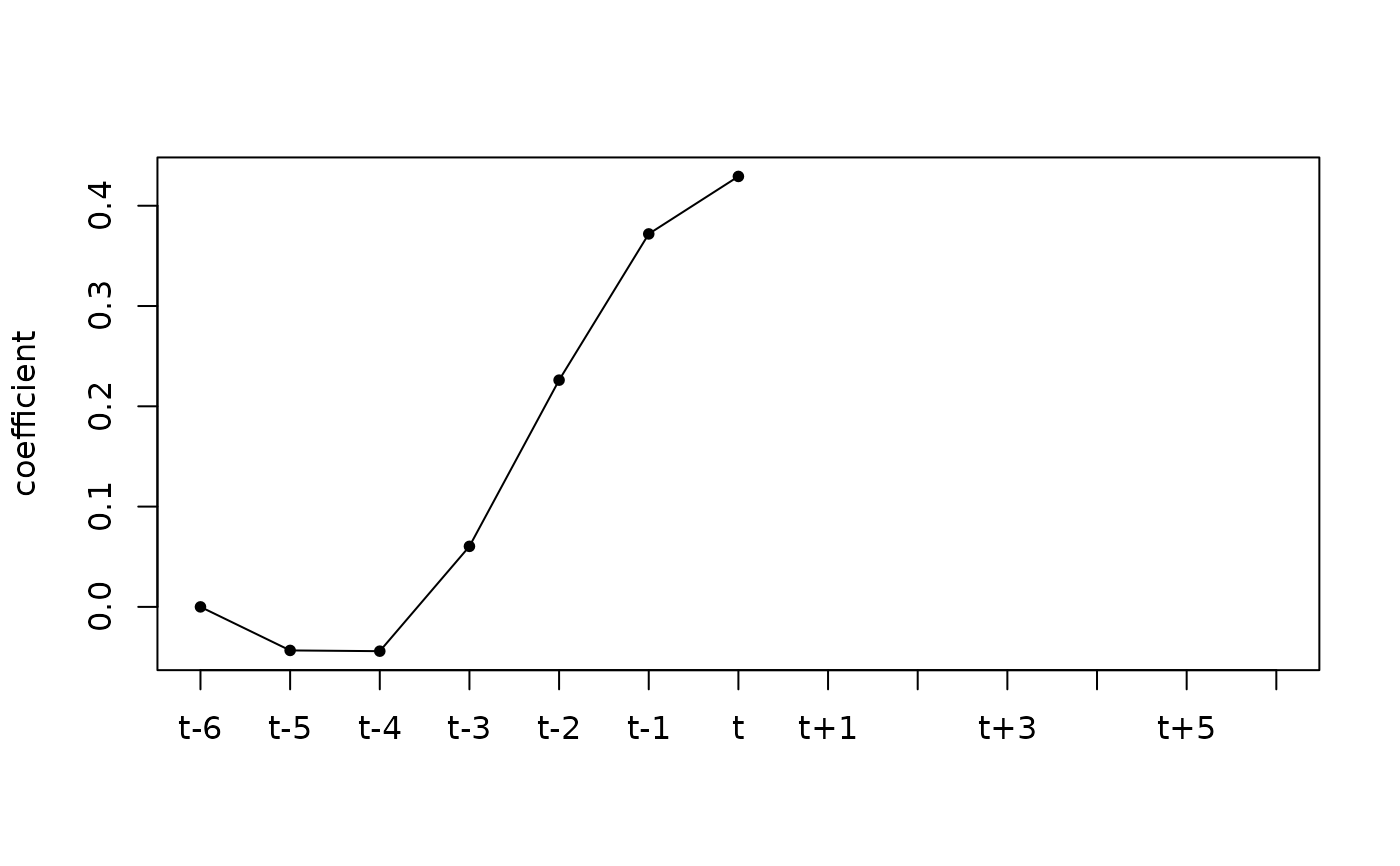
rkhs <- rkhs_filter(horizon = 6, asymmetricCriterion = "Timeliness")
plot_coef(rkhs)